Relative vs. Absolute Buoyancy
When an isolated region of a fluid becomes warmer and less dense than its surroundings, it experiences an upward oriented force. This force is commonly referred to as buoyancy. The same principle applies to a balloon that is dragged to the bottom of a swimmming pool - the air contained within the balloon is less dense than the water surrounding the balloon, and the balloon will accelerate upward toward the pool surface when released.
The air within thunderstorms is locally warmer and less dense than its surroundings, and can therefore move upward at speeds of over 100 mph! The magnitude of the upward acceleration of the air in a thunderstorm (and therefore the strength of the storm) depends on how much warmer the cloud is than its surroundings. But what air do we consider to be the thunderstorm's surroundings? Do we compare the air within the cloud to air immediately surrounding the cloud, or air much further away? A storm in Florida will certainly appear to be stronger if we compare the air temperature within it to frigid "external" air that is over greenland, than if we compare it to balmy air that is over Alabama. The former comparison may seem silly, but for many mathematical formulations of buoyancy in the atmosphere, it is not clear which comparison we should use.
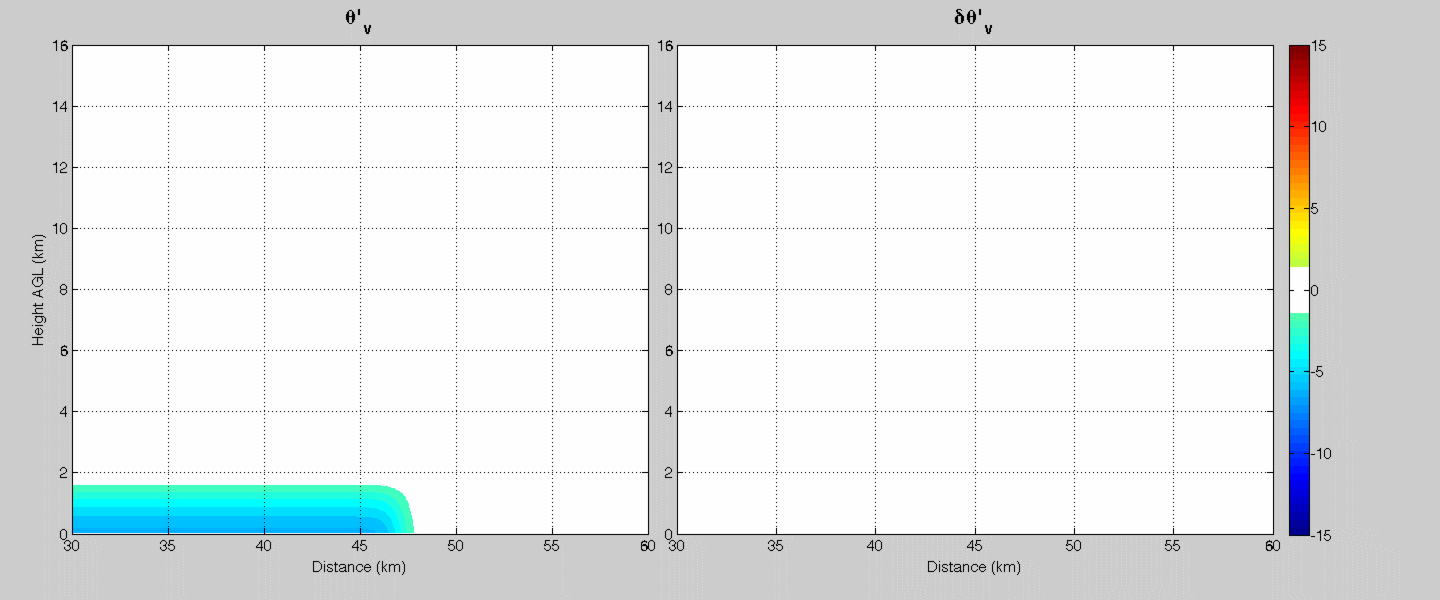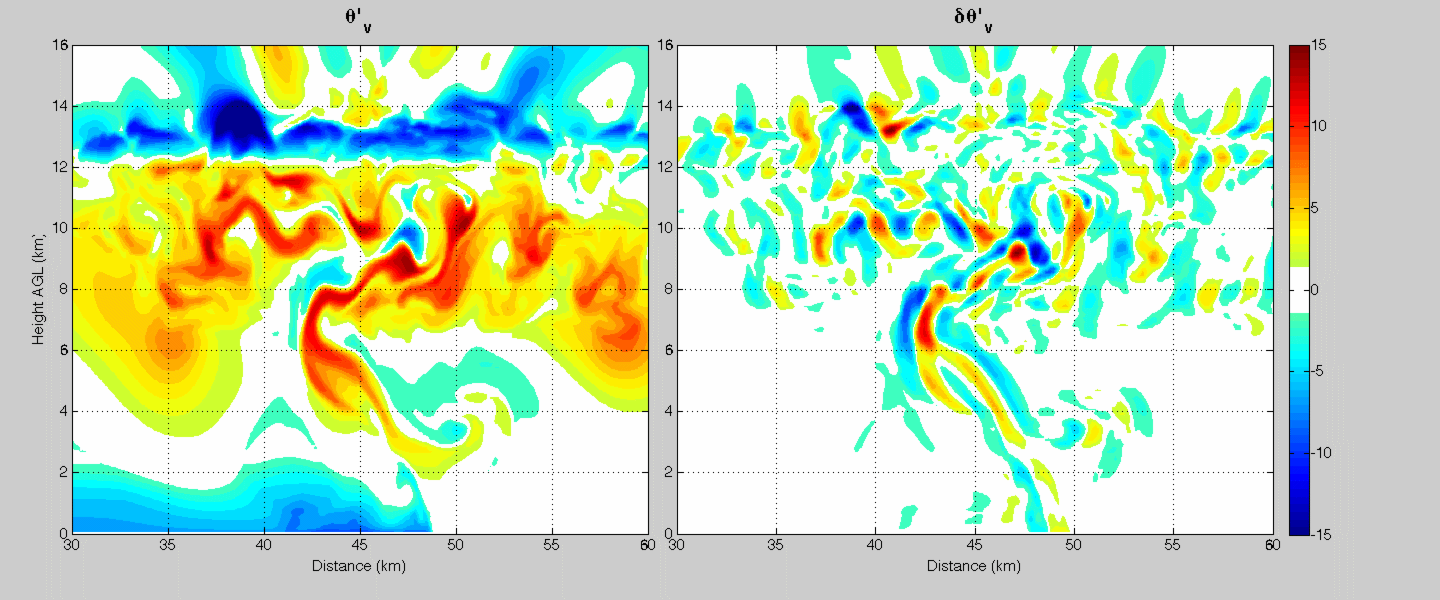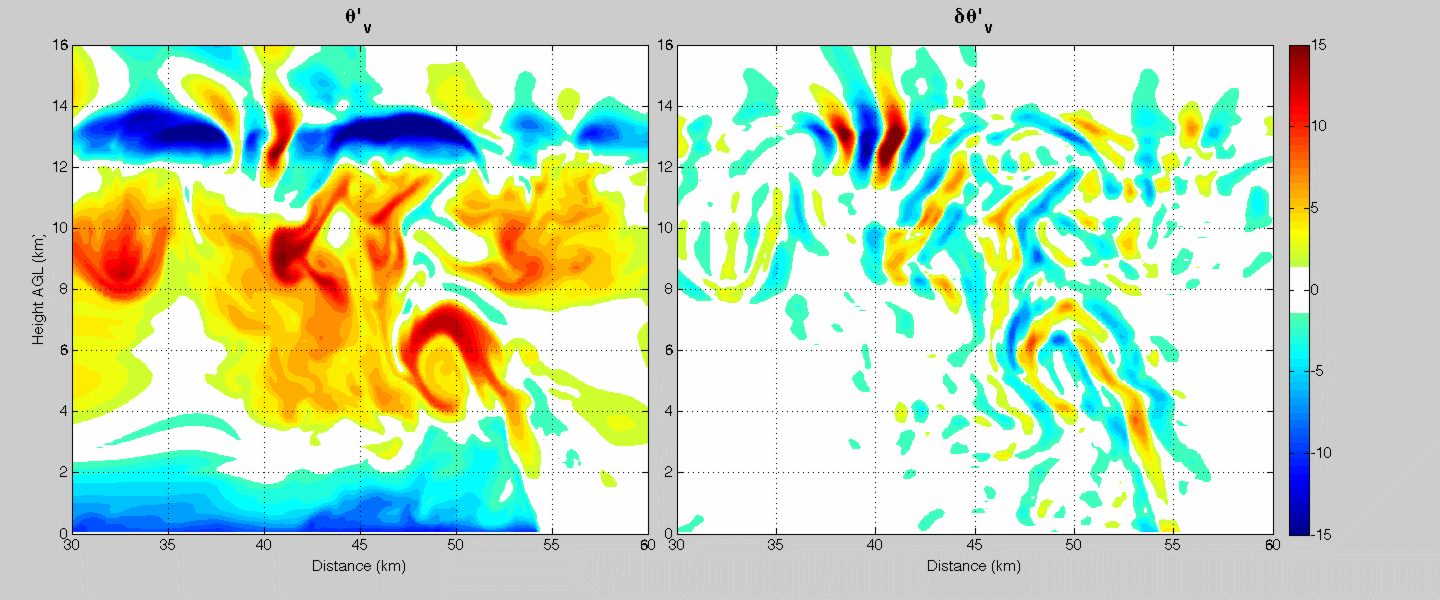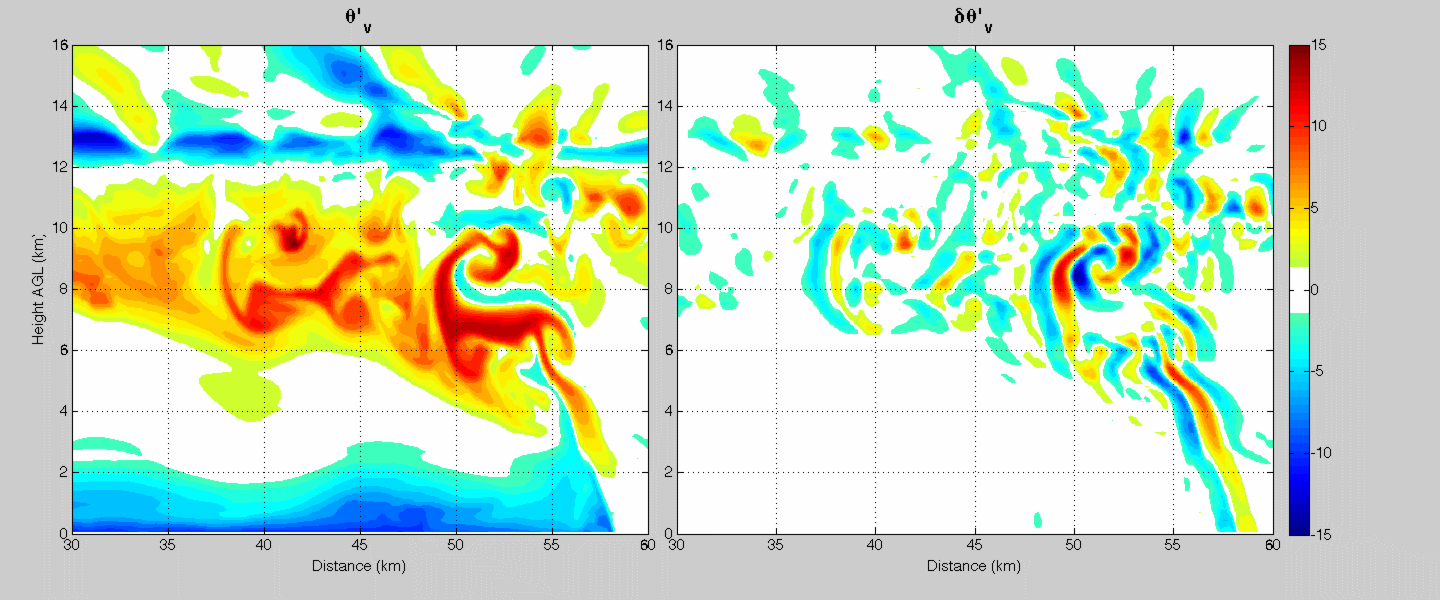
Researchers that study simulations of thunderstorms often diagnose buoyancy (i.e. where parcels should experience upward or downward accelerations) by comparing the temperature of air to the model's inital temperature. The left panel in the animation above shows the temperature difference between air within a simulation of a squall line, and the model simulation's initial temperature. We will call this quantity "absolute buoyancy," since each vertical level within the model is compared to the same initial temperature.
I have shown that buoyancy should really be measured as the temperature difference between air at a given location, and the average of all air at roughly a kilometer horizontal distance away. We will call this quantity the "local temperature difference," or "relative buoyancy" (relative buoyancy is shown in the left panel of the animation above).
Further work is needed to determine how this new view of bouyancy can be used to improve how weather and climate models simulate the effect of moisture, mass, and temperature transports by thunderstorms.


